I wrote my first line of code eight years ago and there is one thing that has not changed since.
My first introduction to programming was watching Daniel Shiffman on YouTube. Daniel is an Arts Professor at NYU, but has a degree in mathematics. The programs he writes generate art, produce mathematical visualizations and simulate nature. While I was completely lost watching the coding, I was intrigued by the visuals produced using simple mathematical equations.
I have not watched Daniel in 4+ years, but was reminded of the artistic aspects of coding after watching a talk given by Dylan Beattie titled The Art Of Code. Dylan details some of the unique art that code can create, and ways in which the code itself can be the art. I would highly recommend this talk for anyone at all interested in this topic.
What I find most interesting about this topic is the way code can be used to visualize mathematics, and how beautiful these visualizations can be. Using simple mathematical equations we can produce intricate, and sometimes infinite, works of art.
The function of art is to hold a mirror up to nature - Douglas Adams
Using mathematics in this way creates the purest forms of art. Mathematics is one of the building blocks of the natural world, and when we use it to produce art we are simply reflecting nature. The art is not influenced by an individual, but is instead a pure representation of the natural world, and its beauty. Code is the mirror that allows us to do this. Without code, these visuals would not be possible.
To illustrate this beauty, I have written three programs. These programs take a mathematical concept and visualize it. Each program is extremely simple, but produces surprisingly complex outputs.
Lorenz Attractor
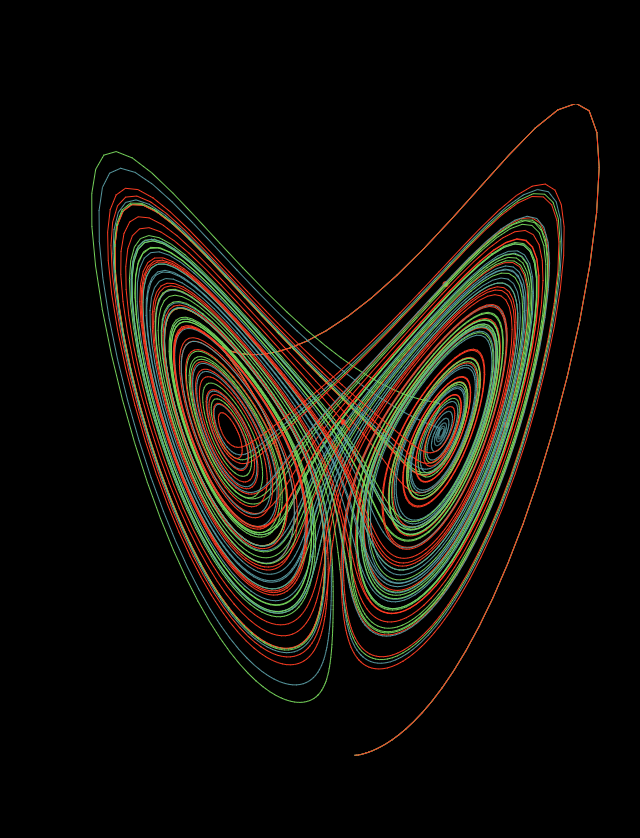
Go here for an animated version.
The Lorenz Attractor illustrates the phenomenon known was the Butterfly Effect (note the shape 🦋 ). The Butterfly effect is a central idea in Chaos Theory. It states that a butterfly flapping its wings can cause a Tornado years later on the other side of the world. The point this is illustrates how sensitive natural systems are. One small change can have profound effects.
The visual you see is made up of three lines: red, green and blue. Each line follows the same equation, with identical initial conditions. However, the lines diverge. This is because each line is rounded differently after each iteration. After enough iterations, the rounding has such a profound effect that the lines become completely diverge. This demonstrates the sensitivity of nonlinear systems, and how one state can greatly influence later states.
Lorenz discovered this phenomenon when attempting to determine why meteorological systems were so hard to forecast. He decided to start by analyzing the simplest model he could think of, consisting of just three differential equations. The Lorenz Attractor is a solution to these equations. Actual systems are much more complex than this, and would amplify this effect even more.
Mandelbrot Set

The Mandelbrot set is the set of complex numbers c for which $z_{n+1} = z_n^2 + c$, does not diverge to infinity. The numbers which are bounded are coloured in black, and the numbers that diverge are coloured based on how quickly they diverge. The image above represents $z = a + bi\ where\ a[-2,0.5]\ and\ b:[-1.5,1.5]$
What is really interesting about the Mandelbrot set is that it is infinite and never repeats itself. You can zoom in anywhere on the set, and you will find a new shape. You can continue to zoom in and continue to find new shapes. Checkout this video for a trippy animation. All this from the colouring of different numbers on the complex plane!
Fractal Tree
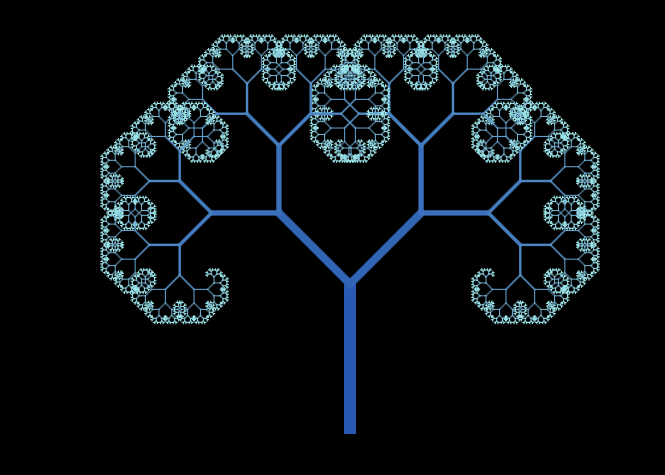
A fractal tree is a great visualization of recursion. The program follows a few simple rules:
- Draw a line
- Move to the end of a line
- Rotate a bit right and draw a line
- Rotate a bit left and draw a line
- Decrease the line size and repeat for both of the new lines
If we do this over and over, we get a fractal pattern in the shape of a tree. A fractal is a geometric patter which repeats itself, potentially forever. Code enables us to make these kinds of things because we can repeat these patterns forever (or at least enough times that it is essentially forever).
Interestingly, the image above is created by only repeating the pattern 12 times! Even with just a few iterations, we can get complex shapes. This was one of my first programs that I ever wrote.
These are just a few examples of algorithmic art. More than anything, I find it intriguing how simple rules can produce such intricate results. This was a nice reminder of all the fun things that are possible with programming, and not every program you write needs to fulfill a business requirement.
Eight years later and I am still writing programs just because I think they look cool. And that is how it should be.
– Mitch
Quote of the Week
Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line. - Benoit Mandelbrot
Favourite Things of The Week
📺 The Art Of Code by Dylan Beattie
🔊 Business Breakdowns Podcast
Detailed insight into unique businesses. So far I have listened to the Facebook and Costco episodes.
📕 On Writing: A Memoir of the Craft by Stephen King
Stephen King is one of the best selling authors of all time and has published more than 77 books. Perhaps he knows a thing or two…